Güvercin Deliği İlkesi Örneği:
SORU: S kümesi
en büyüğü 14 olabilen 6 elamanlı bir pozitif tamsayılar kümesi olsun. Snin boş olmayan altkümelerinin elamanlarının
toplamlarının hepsi birbirinden farklı olamaz. olduğunu gösterin.
İspat:
Bu ifadeyi ispat etmek için en az iki altkümenin
elamanlarının toplamının birbirine eşit olduğunu göstermek yeterli olacaktır.
AÍS
olmak üzere,
sA : Anın elamanlarının toplamı
olsun
Elemanlarının toplamı en küçük olan küme A={1} ve
elamanlarının toplamı en büyük olan küme A={9,10,11,12,13,14}
olur. Bu durumda sAnın alacağı değerler
aşağıdaki gibi ifade edilebilir:
Delik:Altküme
elamanlarının toplamının alabileceği değerler
1≤sA≤69
Güvercin: Bu değerlere karşılık
gelecek altküme sayısı
Boş küme hariç oluşabilecek Altküme
sayısı: 2n-1=26-1=63 olur.
Bu durumda, 63 altküme olmasına karşılık 69 farklı toplama
değeri olabileceğinden her bir altküme elamanlarının toplamının farklı değer
alma olasılığı vardır. Buda ispatı gerçekleştirmez. O zaman S kümesinin 5 veya
daha az elamanlı alt kümelerine bakalım.
|A|≤5 olan
altkümelerde:
Elemanlarının toplamı en küçük olan küme yine A={1} ve
elamanlarının toplamı en büyük olan küme ise A={10,11,12,13,14}
olur. Bu durumda sAnın alacağı değerler
aşağıdaki gibi ifade edilebilir:
Delik:Altküme
elamanlarının toplamının alabileceği değerler
1≤sA≤60
Güvercin: Bu değerlere karşılık
gelecek altküme sayısı
Boş küme ve kendisi(Snin 6 elamanlı tek altkümesi kendisidir) hariç S
kümesinin oluşabilecek 5 elamanlı Altküme sayısı: 2n-2=26-2=61
olur.
Bu durumda, Altküme elamanlarının
toplamları 1 ile 60 arasında maksimum 60 farklı değer alabilmelerine rağmen 61
farklı altküme bulunmaktadır. Güvercin
Deliği ilkesi gereği en az iki altkümenin elamanları toplamı aynıdır.
İspat Bitmiştir.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Güvercin Deliği İlkesi Örneği:
SORU: S={1,2,3,4,5,6,7,8,9} kümesinin 6
elamanlı her hangi bir altkümesinde toplamı 10 olan iki sayı vardır ifadesini
gösteriniz.
İspat:
Bu sorunun cevabında he zaman
toplamı 10 olan en az bir ikili alınması gerektiğini göstermemiz gerekmektedir.
Öncelikle S kümesinde toplamları 10 olan ikili grupları sıralayalım.
1+9=10; 2+8=10; 3+7=10; 4+6=10; ve geriye yalnızca 5 sayısı kalmaktadır. Sonuç olarak 10
toplamasını sağlayan 4 ikili ve ayrı kalan 5 ile 5 grup oluşur.
Delik:
Sayıların seçilebileceği grup sayısı burada 5tir.
Güvercin:
Seçilecek elaman sayısı burada 6dır.
Bu durumda 5 gruptan 6 sayı
almamız gerekmektedir. Güvercin Deliği ilkesine göre en az bir gruptan iki
elaman almamız gerekir. Bu da, her zaman toplamı 10 olan en az bir ikili
seçilecek demektir.
İSPAT BİTMİŞTİR!
--------------------------------------------------------------------------------------------------------------------------------------------------
Ackermann Fonsiyonu:
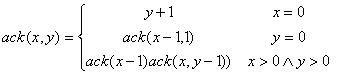
ack(2,2)=ack(1,ack(2,1))
= ack(1, ack(1, ack(1,1)))
= ack(1, ack(1, ack(0,ack(1,0))))
= ack(1, ack(1, ack(0, ack(0,1))))
= ack(1, ack(1, ack(0, 2)))
= ack(1, ack(1, 3))
= ack(1, ack(0,ack(1,2)))
= ack(1, ack(0, ack(0,ack(1,1))))
Daha
önce bulduğumuz gibi ack(1,1)= ack(0,2)=3
= ack(1, ack(0, ack(0, ack(0,ack(1,0)))))
= ack(1, ack(0, ack(0, ack(0,
ack(0,1)))))
= ack(1, ack(0, ack(0, ack(0,
2))))
= ack(1, ack(0, ack(0,3)))
= ack(1, ack(0, 4))
= ack(1, 5)
= ack(0,ack(1,4))
= ack(0, ack(0,ack(1,3)))
= ack(0, ack(0, ack(0,ack(1,2)))))
= ack(0, ack(0, ack(0,
ack(0,ack(1,1))))) Daha
önce bulduğumuz gibi ack(1,1)= ack(0,2)=3
= ack(0, ack(0, ack(0,
ack(0,3))))
= ack(0, ack(0, ack(0,
4)))
= ack(0, ack(0, 5))
= ack(0, 6)
= 7